Математическая модель нервной клетки

Биологическая нейронная теория очень развита и сложна. Чтобы построить математическую модель процессов, происходящих в мозгу, примем несколько предположений:

а) каждый нейрон обладает некоторой передаточной функцией, определяющей условия его возбуждения в зависимости от силы полученных сигналов; кроме того, передаточные функции не зависят от времени;

б) при прохождении синапса сигнал меняется линейно, т.е. сила сигнала умножается на некоторое число; это число будем называть весом синапса или весом соответствующего входа нейрона;

в) деятельность нейронов синхронизирована, т.е. время прохождения сигнала от нейрона к нейрону фиксировано и одинаково для всех связей; то же самое относится ко времени обработки принятых сигналов.

Необходимо заметить, что веса синапсов могут меняться со временем - это принципиальная особенность. Именно изменение этих весов отвечает за возможность различной реакции организма на одни и те же условия в разные моменты времени, т. е. возможность обучения.

Нужно признать, что все эти предположения достаточно сильно огрубляют биологическую картину. Например, время передачи сигнала напрямую зависит от расстояния между нейронами (оно может быть достаточно большим). Тем удивительнее, что при этих упрощениях полученная модель сохраняет некоторые важные свойства биологических систем, в том числе адаптивность и сложное поведение.

Построим математическую модель нейрона (далее мы будем называть ее нейроном). Нейрон — это несложный автомат, преобразующий входные сигналы в выходной сигнал (см. рис. 1.2). Сигналы силы x₁, x₂, . x_n, поступая на синапсы, преобразуются линейным образом, т.е. к телу нейрона поступают сигналы силы w₁*x₁, w₂*x₂, . w_n*x_n (здесь w_i — веса соответствующих синапсов).

Рис. 1.2. Математическая модель нейрона

Для удобства к нейрону добавляют еще один вход (и еще один вес w₀), считая, что на этот вход всегда подается сигнал силы 1. В теле нейрона происходит суммирование сигналов:

Затем применяет к сумме некоторую фиксированную функцию f и выдает на выходе сигнал силы Y = f(S).

Эта модель была предложена Маккалоком и Питтсом еще в 1943 г. При этом использовались пороговые (ступенчатые) передаточные функции (см. рис. 1.3, а), и правила формирования выходного сигнала Y выглядели особенно просто.

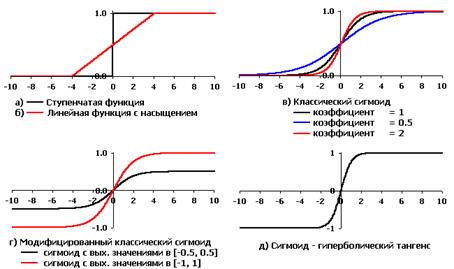
Рис. 1.3. Активационные функции искусственных нейронов,
используемые при моделировании ИНС

В 1960 г. на основе таких нейронов Розенблатт построил первый в мире автомат для распознавания изображений букв, который был назван “перцептрон” (perception — восприятие). Этот автомат имел очень простую однослойную структуру и мог решать только относительно простые (линейные) задачи. С тех пор были изучены и более сложные системы из нейронов, использующие в качестве передаточных любые непрерывные функции.

Одна из наиболее часто используемых передаточных функций называется сигмоидной (или логистической) (см. рис. 1.3, в, г, д) и задается формулой:

Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:

Рис. 1.4. Простейшая нейросеть из трех нейронов

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Множество математических моделей нейрона может быть построено на более простой концепции строения нейрона. На рис.6.3. показана наиболее общая схема. Так называемая суммирующая функция объединяет все входные сигналы
, которые поступают от нейронов-отправителей. Значением такого объединения является взвешенная сумма, где веса
представляют собой синаптические мощности. Возбуждающие синапсы имеют положительные веса, а тормозящие синапсы-отрицательные веса. Для выражения нижнего уровня активности нейронак взвешенной сумме прибавляется компенсация (смещение)
.

Рис.6.3. Простая математическая модель нейрона.

Так называемая функция активации рассчитывает выходной сигнал нейрона

по уровню активности
. Функция активации обычно является сигмоидальной, как показано в правой нижней рамке на рис. 6.4. Другими возможными видами функций активации являются линейная и радиально-симметричная функции, показанные на рис. 6.4.

Рис. 6.4. Функции активации нейронов (возбуждение выходного слоя):

Здесь: а-область возбуждения букв; б-область возбуждения цифр; в- область

возбуждения специальных знаков.

Обучение нейронных сетей

Существует множество способов построения нейронных сетей. Они различаются своей архитектурой и методами обучения.

После завершения обучения нейронная сеть готова к использованию. Это-рабочая фаза. В результате обучения нейронная сеть будет вычислять выходные сигналы, близкие к эталонным данным при соответствующих входных сигналах. При промежуточных входных сигналах сеть аппроксимирует необходимые выходные величины. Поведение нейронной сети в рабочей фазе детерминировано, то есть каждой комбинации входных сигналов на выходе будут одни и те же сигналы. На протяжении рабочей фазы нейронная сеть не обучается. Это очень важно для большинства технических применений, поскольку система не будет стремиться к экстремальному поведению [91].

Собаки Павлова.Как же обучается нейронная сеть? Как правило,это демонстрируется на примере известных собак Павлова. Когда он показывал собакам еду, у них выделялась слюна. В собачьих клетках устанавливались звонки. Когда звонил звоночек, у собак не выделялась слюна, т.е. они не видели разницу между звонком и едой. Тогда Павлов стал обучать собак иначе, каждый раз используя звоночек при предъявлении пищи. После этого, даже при отсутствии еды, наличие звоночка вызывало у собак слюну.

реакции на изображение.

Правило обучения Хебба.Совершенно очевидно, что звонок при предъявлении пищи вырабатывает ассоциацию между ним и едой. Следовательно, выходная линия также становится толще, поскольку увеличивается вес синапса. На результатах этих наблюдений Хебб [81] в 1949 году предложил следующее обучающее правило: Увеличивать вес активного входа нейрона, если выход этого нейрона может быть активным. Уменьшить вес активного входа нейрона, если выход этого нейрона не может быть активным.

Это правило, названное правилом Хебба, предшествует всем обучающим правилам, включая наиболее используемый в настоящее время метод обратного распространения ошибки (errorbackpropagationalgorithm) [81].

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Введение. Классический факторный анализ [1] позволяет на базе выборки различных показателей сформировать факторные показатели с необходимой точностью описывающие исходный объект и уменьшающие размерность задачи путем перехода к ним. Факторные показатели являются линейной комбинацией исходных показателей. Тем самым факторные модели носят линейный характер.

Для восстановлений закономерностей между параметрами используется специальный алгоритм обучения нейронной сети: алгоритм обратного распространения ошибки [7]. Этот алгоритм с математической точки зрения представляет собой градиентный метод оптимизации.

Суть данного метода для построений факторных моделей заключается в том, что для выявления закономерностей между параметрами используется математическая модель нейронной сети с линейной передаточной функцией. Значения факторных переменных определяется равным значениям выходных сигналов нейронов скрытого слоя нейронной сети. Тем самым нейронная сеть осуществляет классический факторный анализ, т.е. строит линейные комбинации исходных параметров [8, 9, 10].

В данной работе предлагается усовершенствованный алгоритм обратного распространения ошибки посредством введения дополнительного слагаемого в функцию ошибки для построения интерпретируемой факторной структуры и решения задачи факторного вращения на базе нейронной сети.

Математическая модель нейрона. Состояние нейрона описывается набором переменных:

Нейронная сеть. Отдельные нейроны объединяются в слои. Выходные сигналы нейронов из одного слоя поступают на вход нейронам следующего слоя, модель так называемого многослойного персептрона (рис. 1). В программной реализации авторской нейронной сети вводится понятие нейронов потомков и нейронов предков. Все нейроны, имеющие входной сигнал от данного нейрона являются его потомками или пассивными нейронами или аксонами. Все нейроны образующие входные сигналы данного нейрона являются его предками или активными нейронами или дендритами.

Рис. 1 . Схема простой нейронной сети (входные нейроны, скрытые нейроны, выходной нейрон).

Алгоритм обратного распространения ошибки. Алгоритм обратного распространения ошибки для обучения нейронной сети соответствует минимизации функции ошибки E ( w _ij ) . В качестве такой функции ошибки может быть использована сумма квадратов отклонений выходных сигналов сети от требуемых:

В данном алгоритме итерация обучения состоит из трех процедур:

Распространение сигнала и вычисление сигналов на выходе каждого нейрона.

Вычисление ошибки для каждого нейрона.

Изменение весов связей.

Путем многократного цикличного подставления наборов сигналов на входе и выходе и обратного распространения ошибки производится обучение нейронной сети. Для многослойного персептрона и определенного вида передаточной функции нейрона, при определенном виде функции ошибки доказана сходимость этого метода [11].

Вычисление ошибок. Если передаточная функция нейронов является сигмоидальной, то ошибки для нейронов различных слоев вычисляются по следующим формулам.

Вычисления ошибок для нейронов выходного слоя производится по формуле:

L – глубина нейронной сети,

Ошибки для нейронов остальных слоев рассчитываются по формуле:

где i – индексы нейронов-потомков данного нейрона,

Изменение пороговых уровней нейронов и весов связей. Для изменения весов связей используется следующая формула:

где i – индекс активного нейрона (нейрона источника входных сигналов пассивных нейронов),

j – индекс пассивного нейрона,

n – номер итерации обучения,

α – коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции,

m – число переменных,

g – число факторов,

В матричном виде линейная модель факторного анализа записывается в виде:

В данном методе построения факторной модели латентные характеристики ставятся в соответствие нейронам скрытого слоя. При этом число нейронов скрытого слоя полагают меньшим числа нейронов входного слоя для осуществления факторного сжатия входной информации. Для оценки числа нейронов скрытого слоя можно применять правило Кайзера классического факторного анализа. Нейронам входного и выходного слоя ставится в соответствие исходные характеристики объектов исследования. Когда передаточная функция нейронов линейна такая конфигурация нейронной сети соответствует классическому факторному анализу (рис. 2).

Рис. 2 . Схема нейронной сети классического факторного анализа (число нейронов входного слоя равно числу нейронов выходного слоя, число нейронов скрытого слоя меньше числа нейронов входного слоя).

Для раскрытия взаимосвязи факторной модели и нейронной сети, воспользуемся формулами получения выходного сигнала нейронов скрытого слоя.

где m – число нейронов входного слоя;

Аналогично для выходного слоя:

g − число нейронов скрытого слоя.

Полученная линейная взаимосвязь переменных соответствует классической модели факторного анализа, в которой факторы являются линейными комбинациями исходных переменных. Задача поиска факторного отображения и значений факторов сводится к задаче поиска весов связей и пороговых уровней нейронной сети. Поскольку факторное отображение и значения факторов являются неизвестными, необходима сеть с промежуточным слоем. Сеть в целом осуществляет тождественное преобразование, т.е. выходной сигнал на i -ом нейроне входного слоя равен выходному сигналу i -го нейрона выходного слоя. Отдельные части сети (входная и выходная часть) соответствуют прямому и обратному факторному отображению.

Теорема .

Тогда выполняется следующее равенство :

g − число нейронов скрытого слоя.

Доказательство :

Для поиска весов нейронной сети необходимо выполнение условия:

Допустим, что производилось изменение только i -го входного сигнала.

Из этих условий следует:

Теорема .

g − число нейронов скрытого слоя.

Доказательство :

Для построения нелинейных главных компонент в качестве передаточной функции может быть выбрана антисимметричная сигмоидальная функция:

Другим вариантом получения интерпретируемого факторного отображения может быть использование специального критерия интерпретируемости [12]. Данный критерий заключается в том, что только одна факторная нагрузка для фиксированной переменной, должна быть близкой к 1, тогда как остальные должны быть близкими к 0. Учет эмпирического критерия интерпретируемости, предлагается осуществить следующим образом: среди факторных нагрузок для фиксированной переменной выбирается максимальная по модулю. Все факторные нагрузки отличные от максимальной уменьшаются по модулю на γ , тогда как максимальная увеличивается на γ .

Для стандартизации входных значений нейронной сети используется линейное преобразование:

Численный эксперимент. В качестве исходных параметров были взяты 15 биофизических показателей для 131 лица с артериальной гипертензией начальной стадии:

индекс массы тела (ИМТ),

частота дыхания (ЧД),

сегментоядерные нейтрофилы (С),

лимфоциты (Л),

конечно-систолический размер левого желудочка (КСР),

конечно-систолический объем левого желудочка (КСО),

конечно-диастолический размер левого желудочка (КДР),

конечно-диастолический объем левого желудочка (КДО),

ударный объем (УО),

минутный объем сердца (МОС),

общее периферическое сосудистое сопротивление (ОПСС),

индекс Хильдебрандта (ИХ),

фракция выброса левого желудочка (ФВ),

фракция укорочения левого желудочка (ФУ).

При обучении нейронной сети на данных артериальной гипертензии начальной стадии содержащих 131 паттерн и 15 переменных с антисимметричной сигмоидальной передаточной функцией и 5-ю нейронами на скрытом слое ошибка, приходящаяся на одну переменную, составляла не более 10% от диапазона значений переменной по выборке. График сходимости процесса обучения представлен на рисунке 3. Под итерацией обучения понимается одна эпоха обучения, когда сети подставляется весь набор паттернов обучения. Под суммарной ошибкой на обучающей выборке понимается сумма ошибок для всех паттернов обучающего множества на одной итерации обучения.

Для проверки эффективности обучения нейронной сети исходное множество входных-выходных значений было разделено на 2 независимых подмножества: обучающее и тестовое. Обучение проводилось на обучающем множестве, а верификация – на тестовом. Ошибка нейронной сети на тестовом множестве является показателем того, насколько точно обучилась нейронная сеть. Относительный объем тестового множества был оценен по формуле [7]:

где W − количество входных параметров.

График изменения суммарной ошибки для паттернов тестового множества при верификации на каждой эпохе процесса обучение представлен на рисунке 4. Под суммарной ошибкой на тестовом множестве понимается сумма ошибок для 20 паттернов тестового множества при процессе верификации на каждой эпохе обучения, т.е. когда для обучения был использован полный набор паттернов обучающего множества, но тестовое множество не участвовало в обучении. На каждой эпохе относительная ошибка для тестового множества больше относительной ошибки для обучающего множества. В пределе, когда ошибка для обучающего множества начинает сходится, возможен эффект переобучения, т.е. значение ошибки при верификации на тестовом множестве начинает не уменьшатся, а расти это связано с тем, что промежуточные точки между точками обучающего множества в многомерном пространстве плохо аппроксимируются восстанавливаемой зависимостью нейронной сети. Рисунок 4 и его график изменения ошибки на тестовом множестве показывает, что эффекта переобучения нет и объем обучающего множества достаточен для количества исходных показателей равным 15. На графики заметны лишь незначительные флуктуации ошибки при дальнейшем обучении на обучающем множестве в процессе сходимости ошибки для обучающего множества.

Из графика видно, что эффекта переобучения не наблюдается, дальнейшее обучение приводит лишь к небольшой флуктуации суммарной ошибки на тестовом множестве.

Рис. 3 . График изменения суммарной ошибки на обучающей выборке (131 паттерн, 15 переменных).

Рис. 4 . График изменения суммарной ошибки на тестовом множестве (20 паттернов, 15 переменных).

Рис. 5 . Собственные значения исходных переменных.

Число нейронов на скрытом слое выбиралось согласно правилу Кайзера факторного анализа, когда число факторов выбирается не больше чем количество собственных значений корреляционной матрицы переменных больших 1. График собственных значений исходных переменных приведен на рисунке 5. В ходе численного эксперимента с данными артериальной гипертензии было установлено, что хорошая обучаемость нейронной сети достигается при числе нейронов в скрытом слое не меньшем верхней границы числа собственных значений исходных переменных по правилу Кайзера. При меньшем числе нейронов в скрытом слое наблюдались значительные ошибки на обучающей выборке и наоборот, чем больше нейронов выбиралось на скрытом слое, тем меньше была ошибка на тестовом и обучающем множестве. Это связано с факторным сжатием и потерей информации на скрытом слое.

С точки зрения совпадения факторных структур ошибка прогноза входного паттерна менее 10% оказалась не критичной и нейронная сеть является достаточно обученной для проведения факторного анализа. Данные факторные структуры подтверждаются предыдущими работами [ 11 ].

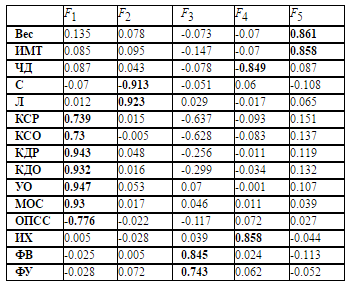
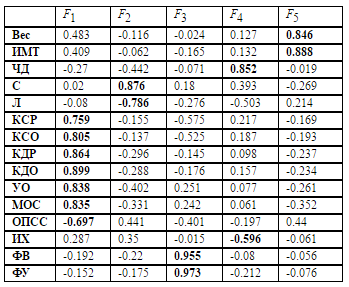
Таблица 3. Факторная структура на базе нейронной сети (критерий интерпретируемости)

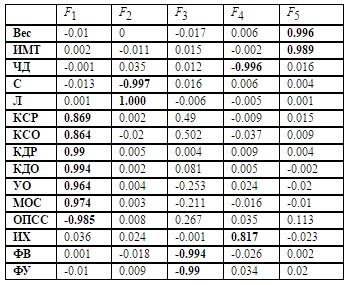
Матрица корреляций факторов немного отличается от ортогональной, что соответствует общему косоугольному случаю (таблица 4 ).

Таблица 4 . Корреляции факторов, полученных на базе нейронной сети

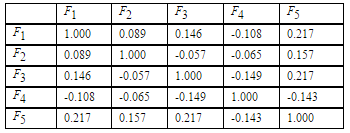
с использованием критерия интерпретируемости

Факторное моделирование позволяет выделить группы взаимосвязанных параметров, образующих факторы заболевания артериальной гипертензии. Факторы проинтерпретированы в ранних работах [ 1 3, 14]:

1. Главный фактор можно интерпретировать как гемодинамический фактор, включающий параметры, описывающие центральную и периферическую гемодинамику. Переменные УО, МОС, ОПСС определяют уровень артериального давления. В норме, изменениям минутного объема циркуляции должна соответствовать адекватная по величине и направлению реакция прекапиллярного русла, которая бы нивелировала эти изменения и сохраняла среднее давление на нормальном уровне. Например, если МО снижен, то артериолы должны сузиться. Если МО увеличен, то артериолы должны расшириться. Нарушения взаимосвязи этих показателей лежат в основе изменений уровня АД. Вместе с тем изменение уровня артериального давления взаимосвязано с модуляцией сердца, за которую отвечают параметры КСР, КСО, КДР, КДО.

2. Фактор составленный из параметров Фракция выброса левого желудочка и Фракция укорочения ЛЖ можно считать важным для непосредственной оценки контрактильной (сократительной, нагнетательной) функции левого желудочка. Этот фактор определяет объемную ресурсоемкость ЛЖ. Он показывает, насколько использованы объемные резервы самого сердца для поддержания уровня артериального давления.

3. Фактор, отвечающий за соответствие массы и роста.

4. Фактор, характеризующий уровень слаженности работы сердца и легких, определяется через частоту дыхания и индекс Хильдебранта.

5. Иммунологический фактор, который может отражать психосоматическое состояние индивида, поскольку этот фактор активируется в стрессовых состояниях. Основной вклад в формирования этого фактора вносят сегментоядерные нейтрофилы и лимфоциты.

Выделенные факторы являются различными аспектами заболевания. Например, это может быть такой фактор риска как ожирение и нарушение фактора 3. Факторы 4 и 5 соответствуют стрессовой восприимчивости, при которой нарушается иммунологический фактор и фактор слаженности работы сердца и легких. Все выделенные факторы подтверждены независимыми медицинскими исследованиями.

В ранней работе [13] даны рекомендации по нормализации выделенных факторов. Выделенные пять факторов позволяют указать группу параметров, на которую нужно воздействовать, чтобы получить максимальный эффект от лечения. Например, для стабилизации уровня артериального давления следует воздействовать на всю группу признаков, описывающих гемодинамический фактор. При этом следует учитывать ремоделирование сердца (структурно-геометрическое состояние) при формировании патофизиологических взаимоотношений в системе кровообращения у пациентов с гипертонической болезнью. Поскольку ожирение является одним из факторов риска, то снижение веса позволит нормализовать фактор, отвечающий за соответствие массы и роста. Исключение стрессовых ситуаций пациентом позволит улучшить показатели, формирующие иммунологический фактор, а также нормализовать фактор, характеризующий уровень слаженности работы сердца и легких.

Заключение. Рассмотрен известный альтернативный метод построения факторной модели на основе нейронной сети и алгоритма обратного распространения ошибки. Данный метод был усовершенствован для проведения факторного вращения и получения интерпретируемого решения. Преимущества данного метода заключается в том, что он объединяет в себе все этапы классического факторного анализа: поиск факторного отображения, факторное вращение и вычисление значений факторов. Этот метод осуществляет косоугольный факторный анализ, тем самым имеет максимальную степень общности для линейной модели.

Иберла К. Факторный анализ. Пер. с нем. В. М. Ивановой; Предисл. А. М. Дуброва. — М.: Статистика, 1980.

Гаврилевич М. Введение в нейроматематику. // Обозрение прикладной и промышленной математики. М.: ТВП, 1994.

Hornik K., Stinchcombe M., White H. Multilayer Feedforward Networks are Universal Approximators. // Neural Networks, 1989, v.2, N.5.

Cybenko G. Approximation by Superpositions of a Sigmoidal Function. // Mathematics of Control, Signals and Systems, 1989, v.2.

Funahashi K. On the Approximate Realization of Continuous Mappings by Neural Networks. // Neural Networks. 1989, v .2, N .3, 4.

Горбань А.Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей. // Сибирский журнал вычислительной математики / РАН. Сиб. отделение. – Новосибирск, 1998. – Т.1, №1. – с. 11-24.

Хайкин C . Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.

Осовский С. Нейронные сети для обработки информации . М.: Финансы и статистика, 2002, 344 с.

Gorban A., Kegl B., Wunsch D., Zinovyev A., Principal Manifolds for Data Visualisation and Dimension Reduction // Springer, Berlin – Heidelberg – New York, 2007.

Kruger U., Antory D., Hahn J., Irwin G.W., McCullough G. Introduction of a nonlinearity measure for principal component models. // Computers & Chemical Engineering, 29 (11-12), 2355–2362 (2005)

Jain A.K., Mao J., Mohiuddin K.M. Artificial Neural Networks: A Tutorial. Computer, March, 1996, pp. 31-44.

Шовин В.А., Гольтяпин В.В. Методы вращения факторных структур. // Математические структуры и моделирование. 2015. № 2. С. 75-84.

Гольтяпин В.В., Шовин В.А. Косоугольная факторная модель артериальной гипертензии первой стадии. // Вестник Омского университета. 2010. № 4. c . 120-128.

Шовин В.А. Конфирматорная факторная модель артериальной гипертензии. // Компьютерные исследования и моделирование. 2012. Т. 4. № 4. c . 885-894.

где в общем случае нелинейная функция преобразования f(u_i) называется функцией активации. Коэффициенты w_ij соответствуют весам синаптических связей: положительное значение w_ij – возбуждающим, отрицательное w_ij – тормозящим синапсам, w_ij = 0 означает отсутствие связи между i – м и j – м нейронами.

Функция активации ФН – это пороговая функция вида

хотя в принципе набор используемых в моделях нейронов f(u) достаточно разнообразен (табл. 2.1), поскольку их свойства, особенно непрерывность, оказывают значительное влияние на выбор способа обучения нейрона (подбор w_ij). Наиболее распространенными функциями активации являются пороговая, линейная (в том числе с насыщением) и сигмоидальные – логистическая и гиперболический тангенс (рис. 2.2). Заметим, что с уменьшением a сигмоиды становятся более пологими, а при a®¥ превращаются в пороговую и сигнатурную функции соответственно. В числе их достоинств следует также упомянуть относительную простоту и непрерывность производных и свойство усиливать слабые сигналы лучше, чем большие.

Функции активации нейронов

Персептрон

Простой персептрон – это ФН МакКаллока–Питтса со структурой рис. 2.1 и соответствующей стратегией обучения. Функция активации – пороговая, вследствие чего выходные сигналы могут принимать только два значения

где для выходного сигнала сумматора

Обучение – с учителем по правилу персептрона в соответствии с алгоритмом:

3) если y_i = 0, а d_i = 1, то w_ij(t+1) = w_ij(t)+x_j, где t – номер итерации;

4) если y_i = 1, а d_i = 0, то w_ij(t+1) = w_ij(t)–x_j.

где d_i, y_i могут принимать любые значения.

Минимизация различий между фактическими y_i и ожидаемыми d_i выходными сигналами нейрона может быть представлена как минимизация некоторой (целевой) функции погрешности E(w), чаще всего определяемой как

где р – количество обучающих выборок. Оптимизация E(w) по правилу персептрона является безградиентной, при большом р количество циклов обучения и его длительность быстро возрастают без всякой гарантии достижения минимума целевой функции. Устранить эти недостатки можно только при использовании непрерывных f(u) и E(w).

Сигмоидальный нейрон

Структура – ФН МакКаллока–Питтса (рис. 2.1).

Обучение – с учителем путем минимизации целевой функции (2.6) с использованием градиентных методов оптимизации, чаще всего алгоритма наискорейшего спуска (АНС). Для одной обучающей пары (р=1) j–я составляющая градиента согласно (2.4), (2.6) имеет вид:

либо аналоговым способом из решения разностного уравнения

где h, m Î (0,1) играют роль коэффициентов обучения, от которых сильно зависит его эффективность. Наиболее быстрым (но одновременно наиболее трудоемким) считается метод направленной минимизации с адаптивным выбором значений h, m.

Следует отметить, что применение градиентных методов обучения нейрона гарантирует достижение только локального экстремума, который для полимодальной E(w) может быть достаточно далек от глобального минимума. В этом случае результативным может оказаться обучение с моментом (ММ)